2.2. Nonnparametric Regression

Nonparametric regression is a data-driven alternative to least squares in which the predictor does not take a predetermined form. Kernel regression estimates the response by convolving the data with a kernel function to combine the influence of the individual data points.

2.2.1. Nadaraya Watson Regression

An example of kernel regression is the Nadaraya-Watson regressor. The Nadaraya-Watson regressor estimates the response \(y\) using a kernel weighted average of the individual datapoints \((x_i, y_i)\):

\[\hat{y}(x) = \frac{ \sum_i K(x, x_i) Y_i }{ \sum_j K(x, x_j) }\]

where \(K(x, x')\) is a kernel function.

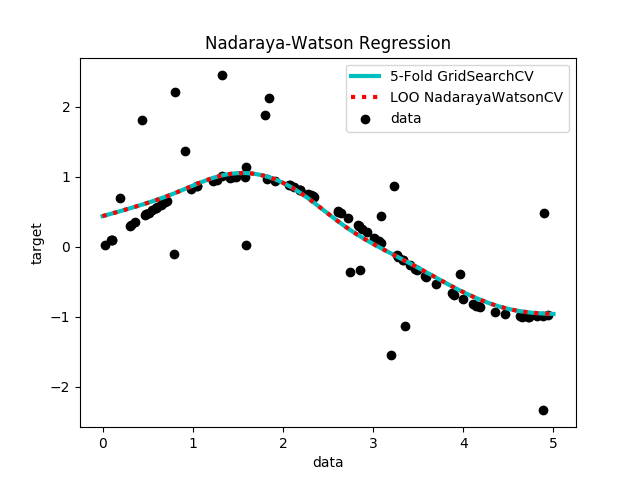
../_images/sphx_glr_plot_nadaraya_watson_0011.png

The model learned by NadarayaWatson MORE

2.2.2. Efficient Leave-one-out Cross-Validation

An advantage of the Nadaraya-Watson regressor is that it allows us to perform leave-one-out cross validation in a single evaluation of the regressor. This is useful because often the kernel function \(K(x, x')\) is parameterized by a bandwidth parameter, say \(h\) that controls the width of the kernel. The Nadaraya-Watson regressor can be written as \(\hat{y}(x) = \omega Y\), where:

\[\omega_i = \frac{ K(x, x_i) }{ \sum_j K(x, x_j) }\]

MORE TO COME!!!

Examples